Difference between revisions of "Quadrupedal Mechanics - Anatomy & Physiology"
| Line 18: | Line 18: | ||
'''What this machine is made of: passive and active tissues''' | '''What this machine is made of: passive and active tissues''' | ||
| − | + | [[File:Fig 2.1.png|thumb|'''2.1 Tissues of the musculoskeletal system.''']] | |
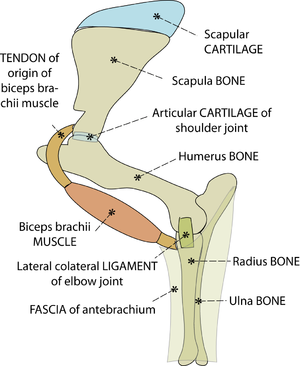
The tissues of the musculoskeletal system are bone, cartilage, ligament, tendon, fascia and muscle (Fig. 2.1). | The tissues of the musculoskeletal system are bone, cartilage, ligament, tendon, fascia and muscle (Fig. 2.1). | ||
The non-muscular parts support the body passively by resisting forces that are applied to the body from outside (extrinsic) or those that are created intrinsically within the body. The most significant extrinsic forces are the earth's gravitational force on the mass of the animal, and the reaction of the ground. An animal, once it is born, must spend most of its life battling with gravity and the problems of contact with ground surfaces. | The non-muscular parts support the body passively by resisting forces that are applied to the body from outside (extrinsic) or those that are created intrinsically within the body. The most significant extrinsic forces are the earth's gravitational force on the mass of the animal, and the reaction of the ground. An animal, once it is born, must spend most of its life battling with gravity and the problems of contact with ground surfaces. | ||
| Line 24: | Line 24: | ||
Animals also derive support from the activity of their muscles, as evidenced from the inability of an anesthetised animal to stand. This active type of support will be discussed in Sections 4 and 5. | Animals also derive support from the activity of their muscles, as evidenced from the inability of an anesthetised animal to stand. This active type of support will be discussed in Sections 4 and 5. | ||
| − | + | ::2.1 Tissues of the musculoskeletal system. | |
| − | + | ::This is a stylised view of the lateral aspect of the proximal left forelimb of the sheep. The skeleton is made of bones and cartilages. A combination of ligaments, muscles & tendons, and sheets of fascia, examples of which are shown, hold these together. Without these soft tissues around them, the jointed bones will not support the weight of the sheep. | |
| − | + | :: | |
| − | This is a stylised view of the lateral aspect of the proximal left forelimb of the sheep. The skeleton is made of bones and cartilages. A combination of ligaments, muscles & tendons, and sheets of fascia, examples of which are shown, hold these together. Without these soft tissues around them, the jointed bones will not support the weight of the sheep. | ||
'''The elasticity of tissues''' | '''The elasticity of tissues''' | ||
| Line 36: | Line 35: | ||
Elasticity is measured by determining the effect of stress, defined as force per unit area, on the shape of the material. When this stress acts in only one direction, this shape change is measured as strain, the distortion per original unit distance, expressed as a percentage. | Elasticity is measured by determining the effect of stress, defined as force per unit area, on the shape of the material. When this stress acts in only one direction, this shape change is measured as strain, the distortion per original unit distance, expressed as a percentage. | ||
| + | [[File:Fig 2.2.png|thumb|'''2.2 Stress, strain and elastic energy''' ]] | ||
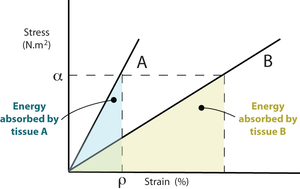
| − | At a particular percentage of strain, | + | At a particular percentage of strain, ρ, a stiffer material will store more elastic energy than a more elastic tissue. Suppose that at this strain percentage, the material can no longer be deformed without damage. Fracture will occur, and because the stiffer material releases more energy it will shatter rather that suffering a simple break. Bone fractures are discussed later in Chapter 3. |
| − | |||
| + | ::2.2 Stress, strain & elastic energy | ||
| + | ::Two linearly elastic tissues A and B have stress - strain curves as shown. At any given value of stress, ρ, the energy absorbed by A, represented here by the area beneath the curve, is less than that absorbed by B. A is stiffer than B. If A and B were bones, A would be the more mineralised. | ||
| + | :: | ||
| − | |||
Revision as of 11:16, 4 March 2013
1 Introduction
Anatomy should be studied using mechanical principles
It is debatable whether the mysteries of life can be interpreted entirely by physical laws, but it is unquestionably true that life cannot be understood without reference to these laws. Thus we cannot interpret, for instance, the nature of an injury to the suspensory ligament of a horse, or the symptoms of a congenital abnormality of the hip of a dog, unless we understand the reason for the particular design of these structures in the normal living animal. The description of structure alone, as encountered in most textbooks of veterinary anatomy, is less interesting and more difficult to learn. Crushed under a load of facts, the student quickly discovers there is no incentive to reason for her or himself.
By applying mechanical principles to the musculoskeletal system of quadrupeds, this book attempts to explain the complexities of body structure. Hopefully, the reader will also gain a greater appreciation of the beauty of animal form and function. Of course, the ideas expressed here are not the last word on the subject. If argument is provoked, this book will be serving its purpose all the more.
The animal machine
A machine is a device for applying forces; an animal is therefore a machine. Force is developed in an animal's muscles, and is transmitted to its site of application by the supporting tissues composed of bone, cartilage, tendon and ligament. These tissues together form the musculoskeletal system.
The animal machine has some remarkable properties not found in man-made machines. Try to envision something man-made that grows without interruption to function, that if damaged or fatigued it can repair itself by replacement of component parts, frequently with little impairment to function, that can adjust in response to demand, such as adaptation to exercise, and that is constructed to last literally a life time. As well, the animal machine can also be a source of pleasure to those who participate in or view athletic performances. And last, we usually take it for granted that the animal machine should contribute in no small way to world agriculture, trade and nutrition: some parts of this machine are good to eat.
No matter how you view it, this book deals with an extraordinary machine.
2 Elasticity: external forces and stored energy
What this machine is made of: passive and active tissues
The tissues of the musculoskeletal system are bone, cartilage, ligament, tendon, fascia and muscle (Fig. 2.1). The non-muscular parts support the body passively by resisting forces that are applied to the body from outside (extrinsic) or those that are created intrinsically within the body. The most significant extrinsic forces are the earth's gravitational force on the mass of the animal, and the reaction of the ground. An animal, once it is born, must spend most of its life battling with gravity and the problems of contact with ground surfaces.
Animals also derive support from the activity of their muscles, as evidenced from the inability of an anesthetised animal to stand. This active type of support will be discussed in Sections 4 and 5.
- 2.1 Tissues of the musculoskeletal system.
- This is a stylised view of the lateral aspect of the proximal left forelimb of the sheep. The skeleton is made of bones and cartilages. A combination of ligaments, muscles & tendons, and sheets of fascia, examples of which are shown, hold these together. Without these soft tissues around them, the jointed bones will not support the weight of the sheep.
The elasticity of tissues
An appreciation of the concept of elasticity is essential to understanding the mechanics of animals.
All materials are elastic to a lesser or a greater extent, even tissues like bone that seem to be stiff rather than elastic. The stiffness is only relative. After being deformed by an external force, all tissues must return to their original shape. If they did not, the body would be permanently deformed. Elasticity is a special function of the passive musculoskeletal tissues.
Elasticity is measured by determining the effect of stress, defined as force per unit area, on the shape of the material. When this stress acts in only one direction, this shape change is measured as strain, the distortion per original unit distance, expressed as a percentage.
At a particular percentage of strain, ρ, a stiffer material will store more elastic energy than a more elastic tissue. Suppose that at this strain percentage, the material can no longer be deformed without damage. Fracture will occur, and because the stiffer material releases more energy it will shatter rather that suffering a simple break. Bone fractures are discussed later in Chapter 3.
- 2.2 Stress, strain & elastic energy
- Two linearly elastic tissues A and B have stress - strain curves as shown. At any given value of stress, ρ, the energy absorbed by A, represented here by the area beneath the curve, is less than that absorbed by B. A is stiffer than B. If A and B were bones, A would be the more mineralised.
| This article is still under construction. |