Quadrupedal Mechanics - Anatomy & Physiology

Introduction

Anatomy should be studied using mechanical principles

It is debatable whether the mysteries of life can be interpreted entirely by physical laws, but it is unquestionably true that life cannot be understood without reference to these laws. Thus we cannot interpret, for instance, the nature of an injury to the suspensory ligament of a horse, or the symptoms of a congenital abnormality of the hip of a dog, unless we understand the reason for the particular design of these structures in the normal living animal. The description of structure alone, as encountered in most textbooks of veterinary anatomy, is less interesting and more difficult to learn. Crushed under a load of facts, the student quickly discovers there is no incentive to reason for her or himself.

By applying mechanical principles to the musculoskeletal system of quadrupeds, this book attempts to explain the complexities of body structure. Hopefully, the reader will also gain a greater appreciation of the beauty of animal form and function. Of course, the ideas expressed here are not the last word on the subject. If argument is provoked, this book will be serving its purpose all the more.

The animal machine

A machine is a device for applying forces; an animal is therefore a machine. Force is developed in an animal's muscles, and is transmitted to its site of application by the supporting tissues composed of bone, cartilage, tendon and ligament. These tissues together form the musculoskeletal system.

The animal machine has some remarkable properties not found in man-made machines. Try to envision something man-made that grows without interruption to function, that if damaged or fatigued it can repair itself by replacement of component parts, frequently with little impairment to function, that can adjust in response to demand, such as adaptation to exercise, and that is constructed to last literally a life time. As well, the animal machine can also be a source of pleasure to those who participate in or view athletic performances. And last, we usually take it for granted that the animal machine should contribute in no small way to world agriculture, trade and nutrition: some parts of this machine are good to eat.

No matter how you view it, this book deals with an extraordinary machine.

Elasticity: external forces and stored energy

What this machine is made of: passive and active tissues

Fig. 2.1 Tissues of the musculoskeletal system.

The tissues of the musculoskeletal system are bone, cartilage, ligament, tendon, fascia and muscle (Fig. 2.1). The non-muscular parts support the body passively by resisting forces that are applied to the body from outside (extrinsic) or those that are created intrinsically within the body. The most significant extrinsic forces are the earth's gravitational force on the mass of the animal, and the reaction of the ground. An animal, once it is born, must spend most of its life battling with gravity and the problems of contact with ground surfaces.

Animals also derive support from the activity of their muscles, as evidenced from the inability of an anesthetised animal to stand. This active type of support will be discussed in Sections 4 and 5.

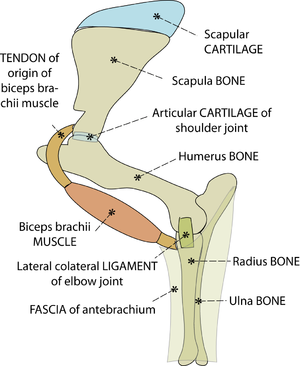
Fig. 2.1 Tissues of the musculoskeletal system

This is a stylised view of the lateral aspect of the proximal left forelimb of the sheep. The skeleton is made of bones and cartilages. A combination of ligaments, muscles & tendons, and sheets of fascia, examples of which are shown, hold these together. Without these soft tissues around them, the jointed bones will not support the weight of the sheep.

The elasticity of tissues

An appreciation of the concept of elasticity is essential to understanding the mechanics of animals.

All materials are elastic to a lesser or a greater extent, even tissues like bone that seem to be stiff rather than elastic. The stiffness is only relative. After being deformed by an external force, all tissues must return to their original shape. If they did not, the body would be permanently deformed. Elasticity is a special function of the passive musculoskeletal tissues.

Elasticity is measured by determining the effect of stress, defined as force per unit area, on the shape of the material. When this stress acts in only one direction, this shape change is measured as strain, the distortion per original unit distance, expressed as a percentage.

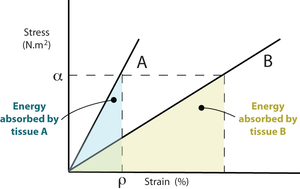
Fig. 2.2 Stress, strain and elastic energy

At a particular percentage of strain, ρ, a stiffer material will store more elastic energy than a more elastic tissue. Suppose that at this strain percentage, the material can no longer be deformed without damage. Fracture will occur, and because the stiffer material releases more energy it will shatter rather that suffering a simple break. Bone fractures are discussed later in Chapter 3.

Fig. 2.2 Stress, strain & elastic energy

Two linearly elastic tissues A and B have stress - strain curves as shown. At any given value of stress, ρ, the energy absorbed by A, represented here by the area beneath the curve, is less than that absorbed by B. A is stiffer than B. If A and B were bones, A would be the more mineralised.

Fig. 2.3 Elasticity

When an elastic material is strained, work is done on it and energy is stored in it. Elastic energy is a form of potential energy. A rubber ball falling on to a hard surface converts what was previously kinetic energy into elastic energy on impact. This elastic energy is released again as kinetic energy when the ball bounces. The ball does not, however, attain the same height as previously. The elastic framework of an animal’s body behaves similarly, as it bounces up and down during running (Fig. 2.4). Some of the kinetic energy is lost as heat. The less energy lost in this way, the greater the elastic resilience of the material. Resilience is the work recovered from a material in elastic recoil, expressed as a percentage of the work previously done in straining it (Fig. 2.5). Passive musculoskeletal tissues should be as resilient as possible, to conserve energy.

Fig. 2.4 Elastic resilience

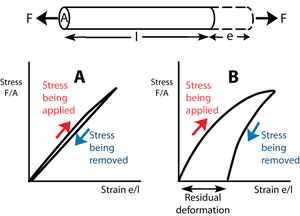
Fig. 2.3 Elasticity

The force F tenses a block of material of transverse sectional area A and length l, producing a deformation e. In Figure 2.3A, stress is proportional to strain. The slope of this line is the elastic modulus.

Upon removal of the stress, the block returns to its original shape. The block is perfectly elastic. In Figure 2.3B, the elastic modulus is not constant; with more stress, a disproportionate deformation is produced.

For this reason, and also because when the stress is removed some of the deformation remains, the block in this instance is imperfectly elastic. Such a residual deformation is not useful in animal mechanics.

Elastic resilience

When an elastic material is strained, work is done on it and energy is stored in it. Elastic energy is a form of potential energy. A rubber ball falling on to a hard surface converts what was previously kinetic energy into elastic energy on impact. This elastic energy is released again as kinetic energy when the ball bounces. The ball does not, however, attain the same height as previously. The elastic framework of an animal’s body behaves similarly, as it bounces up and down during running (Fig. 2.4). Some of the kinetic energy is lost as heat. The less energy lost in this way, the greater the elastic resilience of the material. Resilience is the work recovered from a material in elastic recoil, expressed as a percentage of the work previously done in straining it (Fig. 2.5). Passive musculoskeletal tissues should be as resilient as possible, to conserve energy.

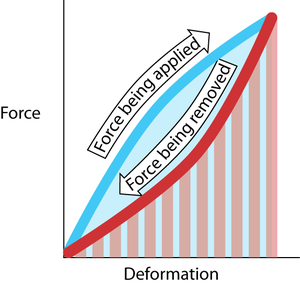
Fig. 2.4 Elastic resilience

The work done in deforming the material is Fd, the product of force and distance. This is the area under the curve made during the application of the force (blue). The work done by the elastic restoring force is the area under the curve made during the removal of the deforming force (red hatching). In this example, these two areas are not the same. The difference in area is the energy lost as heat. The resilience is the red hatched area as a percentage of the blue area.

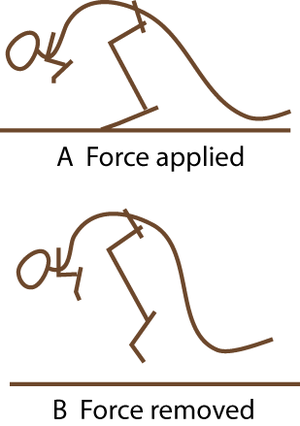
Fig. 2.5 A hopping kangaroo

Compare the angle of the hock joint when the limb bears weight, and when not weight-bearing. The passive tissues supporting this joint store energy in A and release it in B. At hopping speeds of between 10 and 35 km/h, kangaroo locomotion is remarkably efficient. This is due to the almost 100% resilience of the elastic support of the hock joint.

Fig. 2.6 Elastin in the nuchal ligament of a sheep

What makes materials elastic?

The elasticity of materials comes about in several different ways:

Molecular elasticity: Stress may produce a molecular change. The keratinous structures of mammals (hair, wool, hooves and horns) are elastic because the keratin molecule changes from a tight helix to an extended form when it is stretched.

Crystalline elasticity: Stress on a material such as steel results in changes in distances between atoms. A large stress produces only a small distortion. The elasticity is therefore low.

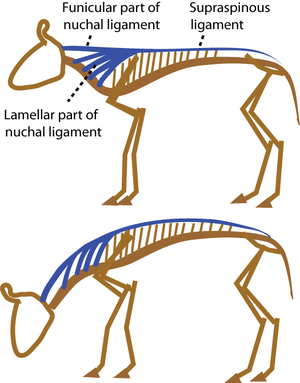
Rubbery elasticity: The elasticity of the most elastic materials results from the cross-linking of long, flexible, convoluted polymers. In rubber, these cross-links are formed by sulphur during the process of vulcanisation. Distortion of a block of rubber results in a distortion of each molecule, which is restored when the stress is removed. Cross-linking is necessary to prevent the molecules from slipping past each other. Elasticity of rubber is lost when there are too many cross-links or when the temperature is too low. Several biological materials show rubbery elasticity. In vertebrates, elastin is present in thin strands in loose connective tissue, providing the extreme elasticity of such tissues as the dermis. It predominates in the middle coat of the wall of large arteries and in the nuchal ligament of herbivores (Figs. 2.6, 2.7). It is not fibrous, but consists of thin homogeneous strands. Its elasticity is similar to that of lightly vulcanised rubber.

Fig 2.7 A grazing cow

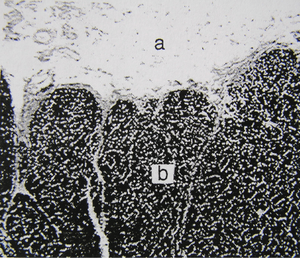
Fig. 2.6 Elastin in the nuchal ligament of a sheep

a. Loose connective tissues surrounding the ligament.

b. Elastin fibres, stained with Verhoeff’s hematoxylin, in the ligament.

Fig.2.7 A grazing cow.

Herbivores have heavy heads held at the end of a long neck. As they flex their neck to graze, the nuchal ligament is strained by 50%. The elastic energy stored is released as the head is raised, so that little muscular effort is needed. A spring loaded garage door borrows this principle from the cow.

Fibrous elasticity: Polymeric molecules derive their elasticity by being arranged partly in ordered patterns to form crystalline regions, and partly with a random arrangement in amorphous regions. Examples of elastic materials of this kind include synthetic textiles like nylon and polyester, and natural ones like silk. Collagen, the main component of the passive musculoskeletal system, also has polymeric molecules, with the crystalline part composed of aligned and cross-linked molecules, appearing as fibrils (Figs. 2.8, 2.9). The molecules are aligned in a specific direction to form fibrils.

Fig. 2.8 Molecular structure of collagen in a tendon, diagrammatic

The significance of collagen

The fibrous elastomer collagen is by far the most predominant passive supporting substance in vertebrates. 20% of the protein of a mouse is collagen. Tendon, ligament and dermis are almost pure collagen, and it is a major constituent of bone and fibrocartilage. Few tissues lack it entirely. Collagen quality is of commercial interest because it determines the tenderness and appropriate cooking methods of different muscles, at different stages of growth.

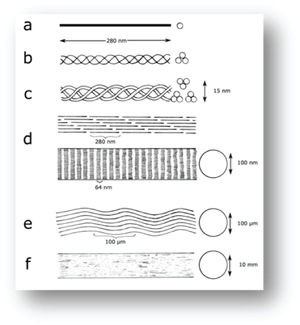
Fig. 2.8 Molecular structure of collagen in a tendon, diagrammatic

Tendon structure as envisaged by:

a., protein chemistry;

b., c., and d., X-ray diffraction;

d., electron microscopy;

e., light microscopy and

f., as seen grossly in a large animal.

Fig. 2.9 Collagen structure, viewed electron-microscopically

Collagen molecules, fibrils and fibres

Collagen fibrils are formed when three tropocollagen molecules, each consisting of three helically arranged polypeptide chains 280 nm long, coil helically together, and align with other such "super helices". These polymeric molecules each overlap about one quarter of their length, so that an axial periodicity of 60-70 nm is visible with the electron microscope (Fig. 2.9). A collagen fibre is formed from bundles of fibrils (Fig. 2.8). Single collagen fibres are visible with the light microscope in connective tissues. They accumulate in bundles or sheets to form the gross structures ligaments, tendons and fasciae.

Fig. 2.9 Collagen structure, viewed electron-microscopically

Magnification x25,000.

Lateral accessoriometacarpal ligament of a horse.

Collagen fibrils, sectioned longitudinally and transversely (from Deane, Massey thesis, 1991).

Collagen matures with age

Stable aggregations of collagen molecules to form fibrils are achieved by cross-linking of the molecules. These give collagen both strength and elasticity. In newly formed collagen, the cross-links are relatively few, but with age, there is a significant increase in the number and the stability of the cross-links. This has two significant effects. Excessive stress on immature collagen contributes to tendon and ligament disease in young animals; the training of horses especially must take the aging of collagen into account. Also, variations in collagen cross-links cause the toughness associated with different cuts of meat, and with the increase in toughness in meat from older animals.

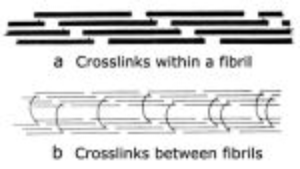
Fig. 2.10 Collagen cross-links

Crosslinks in immature connective tissue pass between collagen molecules within a fibril (a). The molecules are linked head to tail to form an infinite polymer.

In a mature collagen fibre, (b), the crosslinks pass between the fibrils to link them in register.

(Adapted from Bailey, 1988).

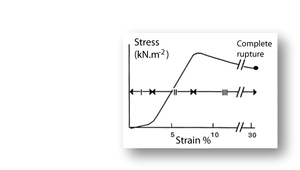
Fig. 11 Tensile stress in collagen

The stress–strain relationship in a bundle of collagen fibres, at a low rate of strain.

Phase I: Rapid elongation as the "crimp" in the collagen fibres is eliminated. This part of the curve is smaller at the high strain rates likely to occur in vivo.

Phase II: Stress is proportional to strain. This elastic phase of collagen is the phase most useful in vivo.

Phase III: Breakdown of the crystalline components of the collagen fibres. Deformation takes place with progressively less stress.

Putting the stress on to collagen

When a collagenous structure, such as tendon, progressively undergoes tensile stress in a laboratory preparation, three stages o stress strain relationships are recognised (Fig. 2.11). During the first stage, the wavy pattern or crimp seen in bundles of fibres is removed. This crimp is probably due to an in–series elastic component, accounting for the high elasticity over this stage. This first stage is less apparent when the strain rate is high. Such a high strain rate is the likely situation in tendon in vivo. The second stage is the true elastic stage for collagen fibres. With stretch, the axial periodicity of the fibres is increased. The elasticity of collagen is about one three hundredth that of elastin. This makes it a suitable material for structures that must withstand large forces without stretching too much. In stage three, there is a loss of elasticity. The crosslinks between the fibrils have been broken by the stress and the material exhibits viscous flow. The strain remains after removal of the stress, defined as residual deformation in Fig 2.3.

Organisation of collagen in bone and fibrocartilage

In both bone and fibrocartilage, collagen fibrils are embedded in a matrix. For bone, the matrix is made of mineral crystals and for cartilage the matrix is mucopolysaccaride. Bone and fibrocartilage are therefore both heterogeneous. Each is a composite material consisting of several different components. In bone, collagen forms one third of the weight and one half of the volume of the tissue. The arrangement of the collagen determines the quality of the bone. In the most structured bone, the collagen fibres are arranged parallel to one another in sheets, or lamellae, 5µm thick (Fig. 2.12). The alignment of the collagen alternates between the lamellae. In some bones, the lamellae form concentric rings around blood vessels. Each set of such rings is called an osteone. Not all bone is, however, lamellar bone; such highly organised bone is only common in larger reptiles and mammals. The predominant component of bone, by weight, is the organic part. Crystals of hydroxyapatite that lie between the collagen fibrils within each lamella form this. The resulting mineralised tissue is one twentieth as elastic as pure collagen in tension. Fibrocartilage contains collagen in a less organised pattern than lamellar bone. The more elastic type of cartilage contains elastin also. The matrix of cartilage is a polymer made up of proteins and polysaccharides in hydrated complexes, known as mucopolysaccharide.

Fig. 2.12 Bone structure

A magnified, schematic view of a section from the shaft of a bovine femur.

a periosteum

b lamellar bone

c osteone

d vascular canal

The advantage and organisation of composite materials

As examples of composite materials, the physical properties of bone and fibrocartilage are unlike those of either component taken alone, and are not the sum of the two taken together. Collagen fibres resist tension forces and hydroxyapatite resists compression forces. The composites, bone and fibrocartilage may therefore be likened to manmade materials such as ferroconcrete, fibreglass or filled rubber. The discovery of these revolutionised construction of bridges, boats and tyres, as was animal construction revolutionised when bony skeletons were invented much longer ago. Structures made up of bone or fibro-cartilage are seldom homogeneously constituted. Their composite materials have specific orientations and densities, resulting in compact or spongy bone, or hyaline cartilage with little collagen or dense fibrocartilage. The elasticities and strengths of these depend on both the orientation of the force to the direction of the fibrous component, or "grain", and the proportions of each component. For instance, bone lamellae are densest around the surface and along the shaft of a bone (Fig. 2.13). The reasons for this are apparent once the forces within the structure are considered.

Fig. 2.13 Structure of a long bone

The architectural requirements specify that only sufficient material should be used to allow for stresses the bone is expected to tolerate. Thus, the extremities are composed of spongy bone internally, the shaft is osseous only on the outside, and the dense laminar bone of the shaft is thickest halfway along its length. During growth, an increase in the length of the bone occurs by ossification of cartilage, produced from the epiphyseal line, in the metaphyseal region. This growth is minimally affected by stresses in tendons and ligaments, because these structures are attached to the epiphyseal regions beyond the epiphyseal lines.

Compression and tensile strength of bone and cartilage

The strength of a tissue is determined by measuring the minimum stress needed to produce permanent deformity in the material. Deformation comes about by pairs of opposing forces that cause compression, tension or shear (Fig 2.14). The compressive strength of fresh compact bone loaded parallel to the grain is about 170 MN.m-2. This is impressive, considering that the compressive strength of marble and granite is little more, at 200MN.m-2. Cartilage has a compressive strength lower than bone.

• Fresh, compact bone loaded parallel to the grain has a tensile strength of 80MN.m-2. For steel it is 500MN.m-2. Again, cartilage has a compressive strength lower than bone.

• The resistance of compact bone to shear may be as low as 50MN.m-2 if stressed parallel to the grain, and as high as 120 MN.m-2 if stressed transversely to the grain. Cartilage, tendon and ligament have less resistance to shear.

If bone is mechanically superior to other materials, why is it not used more often for preference?

Fig. 2.14 Types of stress

Pairs of forces can exert three types of stress on solids

Weight economy and the choice of building materials

In nature, the most successful animal would be expected to economise on the use of building materials. Living in a highly competitive athletic environment, neither the hunter of the hunted can afford the luxury of excessive inertia-producing mass. Wild animals are lean and mean. The successful animal will employ in any given situation the least dense material for the task, in relation to the maximal mechanical demands that are made. With regard to weight economy, therefore, the specifications of the animal machine will use bones where high compression and shear forces are to be resisted, cartilage where these forces are lower and where lightness and elasticity are required, and pure collagen fibres where tensile forces alone are to be resisted. Because animals economise on materials, the size and shape of their various parts indicate to us much about their function. Since its establishment as the first modern science by Vesalius in 1543, anatomy has depended very much on this principle.

Grace and coordination: the significance of strain rate

In locomotion, and when the animal must absorb accidental impact, dynamic, rather than the static physical properties described above are much more relevant. A small stress suddenly applied may do more damage than a large stress gradually applied. To break a piece of string, it is useful to apply a high-tension strain rate (give it a sudden jerk) as well as shear (pull the string over the edge of a table). Bone fractures are more likely when movement becomes less coordinated. The actual strain rate is difficult to measure in the living animal under the conditions in which the supporting tissues are used. Nevertheless, we can appreciate that an animal should run in such a way that strain rates are as low as possible by eliminating hard impact with the ground. Animals generally move smoothly and gracefully.

The advantages and disadvantages of stiffness

A major dynamic physical property of the supporting tissues is their energy absorption ability (Fig. 2.2) or stiffness. The stiffer the material, the less kinetic energy it is able to absorb. Since bones function as levers, stiffness is a desirable property; the higher the proportion of mineral, the stiffer the bone. Bone mineral first appears in bones of the developing fetus at sites where stiffness is needed most. This is either for protection, such as in the cranium to protect the brain from external pressure, or to aid correct development, as in the long bones of the limbs, the shape of which is necessary for the correct form of the muscular system (Fig. 2.15). The most highly mineralised bones in the body are the aptly named petrous temporal bone and the auditory ossicles, both involved in the detection and interpretation of sound waves. These bones assist the process of hearing best if they manage to avoid the absorption of the energy of sound waves. But because of this, they are brittle, and must be protected from other forms of mechanical stress by being enclosed by softer bone.

Fig. 2.15 Ossification of limb bones

These views of a sheep fetus at 38 and 44 days after conception have the mineralised bone stained with alizarin. They show which bones and parts of bones need the stiffening properties of hydroxyapatite crystals to ensure normal development, even though limb bones are not needed to support the weight of the animal at this stage.

Why are the bones of the skull and thorax relatively well developed?

Energy economy – getting the most out of legs

The unmineralised collagenous structures, tendons and ligaments, absorb energy during locomotion as elastic energy, which reappears when the stress is removed, mainly as kinetic energy and partly as heat (Fig. 2.5). The collagen in the limb of a horse behaves like the spring inside a pogo stick (Fig. 2.16). It is the elasticity of legs that offsets for them the inherent disadvantages they have when compared with that unique human invention, the wheel.

Fig. 2.16 Elasticity of collagen"'

Action of the suspensory ligament a.,

the proximal sesamoid bones b,.

and the sesamoidean ligaments c.,

of the fetlock joint d. of the horse at three stages of the stride.

During a fast gallop and when landing from a jump, the ergot on the palmar surface of the fetlock joint contacts the ground

Tissue proportions and the absorption of energy

The greater the mass of a particular material, the more energy it can absorb. The weight of a bone, or for that matter that of the entire skeleton within the body, is understandably dependent more on how much energy need be absorbed during exercise, rather than by the ability to resist a static load. Body design is not well explained by considering only static forces. This will be discussed later in relation to the weight of the skeleton in animals of different body size, in Chapter 7.

The economical design of bones

A bone must contain the minimum material necessary to allow for the combination of compression, tension and shear forces to which it is subjected. Economic gain can be achieved by organising the distribution of ossified and nonossified tissues within a bone, or by designing the shape of the bone to take account of the predominant tension, compression and shear force couples that are applied to it. The next chapter shows how whole scientific disciplines, the osteological aspects of anatomy, archeology and paleontology, are based on this premise.

The design of the passive supporting tissues

Osteology: bones provide long-lasting clues to ancient forces

The study of bones, osteology, is often the only opportunity to deduce the natural history of an animal long since dead. The oldest quadruped bone fossils are 350 million years old (Fig. 3.1). The distribution and density of mineralised tissue indicate the magnitude and direction of the forces acting on a bone in life, no matter how long ago these forces were applied.

Fig.3.1 Ichthyostega

The oldest known tetrapod is a late Devonian amphibian that measured about 1 m in length.

Sculpture within bones

The combination of lightness and compression strength is obtained by internal sculpturing. Trabeculae (Latin, little beams) are oriented parallel to the compression forces. These forces act, for instance, between opposing ends of the bodies of vertebrae, & therefore the trabeculae are parallel to the axis of each vertebral body (Fig. 3.2). At the end of a long bone, the compress-ion force transmitted across a flexed joint is not parallel to the shaft, and will vary in direction. Here, the design most economical of material is a network of interconnecting trabeculae following the compression stress lines (Fig. 2.8). Study the pattern in a long bone that has been sectioned longitudinally.

Fig.3.2 Trabecular compression lines in bone

A median section of the 10th thoracic vertebra of the horse, showing trabeculae within the vertebral body directed along the long axis of the body.

Design to resist bending in one plane

Couples acting in planes parallel to the length of a bone result in bending, which involves a combination of compression (on the inside of the bending curve) and tension (on the outside of the bending curve). If the bending is predominantly in one plane, the shape of the bone is such that the longer dimension is oriented in the same plane as the bending couple. Thus the zygomatic arch is a bony beam turned on edge to the force acting on it, as are the body and the ramus of the mandible, the spinous and the transverse processes of the vertebrae, the scapula, and the wing of the ilium.

Design to resist bending in several planes

The long bones of the limbs, however, must resist bending forces in many directions. Compression and tension due to bending are greatest towards the outside of a bone; hence a hollow cylinder achieves the most strength for the least material. The same principle applies in the design of bamboo and scaffolding. Maximum bending stress occurs half way along the length of the shaft, and here the cortical bone is thicker and denser (Fig. 2.8). An analogous manmade structure is the leafed spring of a car. In this case, one leaf is sufficient at the ends, but all the leaves overlap in the middle of the spring.

Design to resist shearing

Shearing forces are applied to bones at the sites of insertion of tendons and ligaments. Resistance to these forces is enhanced by localised thickenings of the bone. Tubercles such as the ischial tuberosity and the greater trochanter of the femur (Fig. 2.8), which serve to increase the torque of muscles acting about a joint, are large because the shearing stress is great. Couples acting in planes at right angles to the length of a bone result in twisting, which also shears the material. The shearing stress is, as for bending, greatest at the outside, and zero along the central axis of the bone. Hollow shafts give strength with lightness in twisting as well as in bending, and again, such stress is greatest midway along the length of the bone.

Fig.3.3 Attachments of tendons to bone

The direction of the tensile force in the tendon of origin of the biceps brachii muscle of the horse does not change with changing angulation of the shoulder joint, because the tendon bends around the intertuberal groove of the humerus (A). Were this not so, the stress would be concentrated on one part of the junction of bone and tendon (B, arrowed).

The junction of bones with ligaments and tendons

Where tendons and ligaments are attached to a bone, tension, as well as shearing, occurs. At the junction, the collagen fibres of each tissue pass uninterrupted from a mineralised tissue to a non-mineralised tissue. At these junctions, the angle at which tension and shearing occurs must not change with different positions of the limb (Fig. 3.3). This is a special requirement in the design of joints and the location of tendon and ligament attachments .

Elastic energy and bone fractures

Fractures occur when the elastic energy (the area under the stress-strain curve in Fig. 2.2) builds up to a point beyond which any recovery is possible. Highly mineralised bone breaks more easily, for the same percentage of strain. Elastic energy can also be increased by a higher loading rate. Bones fracture most under sudden, violent forces. The same forces applied in a slow, uniform manner would not cause as much injury. A fatigue fracture occurs when muscle fatigue results in, for instance, stumbling, and hence abnormally high loading rates. Damage to bone from external forces depends on the speed, from slight damage due to low speeds of impact, to more damage when an animal is hit by a car, is kicked, or runs into a fence, to the very high energy fractures caused by a bullet.

Kinds of fractures

Bone, we have noted, is stronger under compression than under tension, while shear is intermediate. Appropriate combinations of forces cause tensile fractures (Fig. 3.4 A) in bone mainly at the sites of attachment of tendons and ligaments. Common sites of fracture are, in the horse, the proximal ulna, the patella, the proximal sesamoids, the calcaneus and the accessory carpal bone. Such fractures are usually transverse. Compression fractures, (Fig. 3.4 B) by contrast, are usually oblique, at an angle of 45° that corresponds to the plane of maximal shear stress due to the compressive load. Because bone is damaged more by tension than compression, bending fractures (Fig. 3.4 C) begin on the tension side, are transverse where there is tension, and oblique on the compression side. In torsion fractures, (Fig. 3.4 D) shear stress occurs over the entire shaft of a long bone, and is greatest at the periosteal surface. The result is a spiralling fracture.

3.4 Ways in which a long bone may fracture

The type of external load applied to a bone will determine the pattern of the fracture:

A Tension

B Compression

C Bending (tension and compression)

D Torsion (shear).

The role of tendons

Tendons transmit to bones the force produced by muscles. Muscular force is thereby concentrated on to a small area of the skeleton, contributing to precision of movement and allowing several muscles to act on the same structure in different ways. By the use of tendons, the mass of a muscle may be at a considerable distance from the site of skeletal movement, thereby controlling weight distribution and contours of the body. Consider the insertions of the extensor muscles of the hip joint.

Antifriction devices associated with tendons

Limbs are, of course, not straight, and the angles of joints can change markedly. Tendons allow the transmission of a force round these angles. The simplest way to smooth their passage is to provide a cushion. This is a bursa (Latin, wine sac made of goatskin), a pouch lined by synovial membrane and filled with synovial fluid. This lies between the tendon and the bone (Fig. 3.5 a), or it may wrap around the tendon to form a synovial sheath (Fig. 3.5 b). Sheaths are often held in place by transversely arranged collagenous structures, retinacula. A further adaptation occurs when the surface of the bone becomes changed to articular cartilage and forms one boundary of the bursal cavity. A pulley-like arrangement is formed (Fig 3.5 c).

3.5 Structures reducing friction between tendon and bone

(a) to (d) represent increasing complexity

Left side: longitudinal sections of the tendon

Right side: transverse sections of the tendon

Note that that the opposing surfaces of a synovial space are normally in contact.

a. bursa

b. synovial sheath and retinaculum

c. articular cartilage, bursa and retinaculum

d. sesamoid bone, articular cartilage, synovial joint and collateral sesamoid ligaments

Shearing within tendons

Loaded tendons that are straight sustain only tensile forces, but where a tendon bends shearing forces also occur. Accordingly, tendons compensate by becoming thicker at such places. If forces other than tension are particularly severe, small bones, which are better able to withstand compression and shear, interrupt the tendons. These are called sesamoid bones (Latin, resembling a sesame seed) (Fig. 3.5d, & 3.6). A bone inserted into a tendon also creates the possibility of attaching ligaments to hold the tendon precisely in place. These are collateral sesamoidean ligaments (Fig. 3.6). Both the sesamoid bone, and the bone with which it is in contact, have articular cartilage on their opposed surfaces. This arrangement of a synovial sac interposed between two bony surfaces covered by articular cartilage constitutes a synovial joint. Examples of sesamoid bones in the dog are those interposed in the tendon of insertion of the quadriceps muscle at the stifle joint (the patella) (Fig 3.6), and the bones interposed in the tendon of insertion of the Interosseous muscles at each of the metacarpo- and the metatarsophalangeal joints (the proximal sesamoid bones (Fig. 2.16)). In both these examples, the synovial pouch of the seamoid bone is continuous with the pouch of the adjacent joint.

The lubrication of joints: multigrade specification

The lubrication fluid of bursae, synovial sheaths and joints is secreted from protrusions of synovial membrane, synovial villi, located in loose parts of the joint capsule away from any compressed surfaces. This is synovial fluid. In a normal synovial sac, only a small amount of fluid is present. The viscosity of this clear or pale yellow liquid is more during slow movement, which is when the rate of shear is low. But when the shear rates are highest, the viscosity becomes much lower. The fluid drag and hence the supporting ability of the joint is therefore greatest when the limb is quietly bearing weight; the impedance is conveniently reduced for fast movements. Lubrication is effected in two ways, so that the pressure in the fluid film supports the load. Not only does a film of synovial fluid separate opposing articular surfaces (fluid film lubrication), but also a single layer of glycoprotein molecules of synovial fluid is absorbed into the surface of the articular cartilage and protects the surfaces against wear (boundary lubrication). The resulting lubrication is termed elastohydrodynamic. The cartilage surfaces are elastic; the deformation at contact increases the surface area and the lubricant escapes less readily; and the load-bearing capacity of the joint is greatly increased.

3.6 The largest sesamoid bone

The patella (b) is interposed in the tendon of insertion of the quadriceps muscles (a), that insert on the tibial tuberosity through the patellar ligament (c). The patella is held in place by collateral femoropatellar ligaments (d), and the hinge movement of the joint is maintained by the collateral femorocrural ligaments (e).

The resistance of joint surfaces to wear

Large repetitive compression and shear forces between opposing bones are catered for by an elastic surface 1 to 7mm thick composed of hyaline cartilage. This cartilage is unusual in that it has no perichondrium. The collagen within this articular cartilage differs from that of fibrocartilage in that the fibrils no not aggregate to form fibres. They do, however, align parallel to the surface for a shallow depth over the articular surface, and in a deep, thick zone are perpendicular to the surface and are continuous with the collagen of the underlying bone. Since articular cartilage is 70 to 80% water, its elasticity probably incorporates hydrostatic properties as well. While joints usually cope well with a lifetime of wear, the demands of the breeders and trainers of athletic and working animals are often overoptimistic. Thus injuries to joints arise not only from accidental trauma but also because of genetic selection for high performance, and from overuse.

Orthopedics: assisting natural wear

In various ways, not only joints, but also all other components of the passive musculoskeletal system of these animals can fail. While natural repair is often possible, with rest, diverse orthopedic techniques have been developed to save valuable animals. The application of each of these techniques depends on an understanding of the mechanical principles of the structures needing repair, and the materials used to assist. An orthopedic surgeon constantly depends on good anatomical knowledge.

Force production in animals

A muscle either makes movement, or prevents it: Action or heat?

Forces produced within muscles achieve animal posture and motion. A muscle (Fig 4.1 a, b) consists of a large number of fibres (Fig 4.1 c) arranged in such a way that a force is developed between the two ends of the muscle when the fibres are stimulated by electrical impulses coming from nerves. This force may cause movement, but if the force is no greater than opposing forces either within the animal's body (i.e. from antagonist muscles) or acting externally on the animal's body (such as the force of gravity), no movement will result. Mechanical and heat energy are generated from the chemical energy supplied as nutrients to the muscle. If no movement results from the generation of a muscular force, no mechanical work is done, and all the energy must be released as heat.

Fig. 4.1 Muscle structure 1

The semitendinosus muscle of a dog, as seen by the unaided eye (a & b), and in transverse section with the light microscope (c).

The contractile proteins of muscle

To understand the nature of a muscular force, we must appreciate the molecular and filamentous structure of muscle. Muscle is a machine largely constructed from two proteins, actin and myosin. Actin can exist in a globular form of molecular weight 45,000 and a diameter of 5.5 nm, which readily aggregates to form a long filament (Fig. 4.2 d), each filament contains two strands of spherical actin molecules, twisted on each other. In muscle, the form of these chains is regulated by the presence of two other proteins, troponin and tropomyosin. Myosin is a larger protein, with a molecular weight of 500,000 and a more complex shape. A molecule resembles a thin rod with two small globular “heads” at one end (Fig. 4.2 d). Under the right conditions these molecules aggregate into a sheaf, a cigar shaped structure studded with projections of myosin heads along its length. Because the heads are directed towards the ends of the structure, there is a bare zone in the middle (Fig. 4.2 c). To electron microscopists, the accumulated actin molecules and their associated proteins are known as thin filaments, and the myosin structures as thick filaments. Thin filaments are organised around the thick filaments in a regular hexagonal array. In electron micrographs of muscle, the projections of the thick filaments appear as minute crossbridges that seem to link the thin and the thick filaments.

Fig.4.2 Muscle structure 2

Skeletal muscle fibre in longitudinal section;

a, as visualised by the light microscope;

b & c, by the electron microscope; and

d, as reconstructed from crystallographic X-ray

The appearance of muscle using electron microscopy

Thick filaments are 1.6 µm long, and are joined by a meshwork, anchoring the ends, called a Z disc (Fig. 4.2 c). The serially repeating filamentous array was visible to the early light microscopists, especially using polarised light. They called the region occupied by the thick filaments an anisotrophic or A band, and the region occupied by the thin filaments an isotrophic or I band. The Z disc appeared as a narrow dark band dividing the lighter I bands (Fig. 4.2 b). The whole filamentous structure between adjacent Z discs is called a sarcomere.

What makes the striations in skeletal muscle?

Sarcomeres are added in series along the length of the muscle fibre; a relaxed fibre 3 cm long would contain about 15,000 sarcomeres in series. Within the fibre, the myofilamentous pattern is broken up by other components of the fibre (mainly sarcoplasmic reticulum and mitochondria) to form bundles of myofilaments called myofibrils (Fig. 4.2 b), each about 0.5 µm in diameter. However, the greatest proportion of the transverse sectional area of a muscle fibre, and indeed of an entire muscle, is occupied by myofilaments.

Sliding filaments and the site of the contractile force

Muscle contraction is caused by a sliding of the two sets of filaments past each other. The action sites are the crossbridges between the heads of the myosin molecules and the thin filaments. Crossbridges on opposite ends of the thick filaments are directed in opposite directions. Stimulation of activity at the crossbridges therefore creates a mechanical force tending to bring the thick and thin filaments into greater overlap, decreasing the distance between the Z discs, or sarcomere length, and shortening the muscle. The sarcomere is therefore the fundamental contractile unit of muscle.

Linear motors

A muscle is a linear motor. Most man-made motors are not linear, since they take advantage of the wheel, a device not possible in animals. A man-made machine using a linear motor is the magnetic railway, where a magnetic field both lifts the train off the track, and provides a linear thrust. If we accept the fossil record, the muscle machine preceded electric motors and internal combustion engines, and indeed the also very modern invention of the wheel, by 70 million years.

Fig. 4.3 Sliding filaments in muscle

The sarcomere can normally contract to 44% of its fully stretched length. At its optimal length of 2.2 µm, the thin filaments are maximally in apposition with the crossbridges of the thick filaments.

The force of a muscle depends on sarcomere length

The dimensions of the sarcomere determine the extent to which muscle cells can be stretched or contracted. When fully stretched the sarcomere length cannot exceed 3.6 µm without the fibre losing the ability to contract again (Fig. 4.3). As the muscle contracts, more and more crossbridges are brought into use. The force produced increases (Fig. 4.4) until all the crossbridges between thick and thin filaments can be used. At this point, simply because of the dimensions of the filaments, the sarcomere length is 2.2 µm, i.e. 59% of the fully stretched length. This is the optimal length. With further contraction, no more crossbridges can be used, in fact there is interference by overlapping of thin filaments and the force produced declines. When the sarcomere length is 1.6 µm, the muscle can contract no further without penetration of the Z discs by thick filaments, and resulting damage. The sarcomere, and hence the entire muscle cell in which the sarcomeres are in series, is now 44% of the fully stretched length. These measurements made by electron microscopists can be verified by using a device as simple as a ruler, since they agree with measurements of the range of contraction of muscle fibres (and the macroscopically visible fibre bundles) in the limb muscles of animals.

Fig. 4.4 Tension in muscle

Tension is maximal at a sarcomere length of 2.2 µm. A muscle, therefore, will have only one optimal length for developing tension.

Getting the most out of restricted muscle performance

The stage of contraction at which the force produced by a muscle is optimal is therefore quite limited. The implications of this in the design of the musculoskeletal system will be discussed later in section 7.

Muscle mechanics

Contractile units in series and in parallel

The effect of arranging sarcomeres in series can be visualised by considering two muscles doing work by lifting a weight. In Fig. 5.1 a, a single muscle contracts maximally to lift a weight W through a distance d. If two similar muscles are arranged in series (Fig. 5.1 b), both muscles act equally on the weight. Each contracts the distance d, so the total distance contracted is 2d. The total contractile force is equal to the contractile force of one of them, but by an in-series arrangement, the range of contraction has been doubled.

Similarly, we can consider two muscles in parallel (Fig 5.1 c). When they lift a weight W, each muscle shares the load. Hence each has half the load (W/2) and therefore contracts half the distance (d/2). It would take a load of 2W to make the muscles contract a distance d. So, if sarcomeres in muscle are arranged in parallel this would result in a doubling of the force produced, but the range of contraction in this case would be no greater than that of a single muscle.

Fig 5.1 The effect of the strength of muscles in series and in parallel

A muscle contracts a distance d and lifts a weight W against gravity (a). When two such muscles are in series, the distance lifted is 2d (b). Each muscle is effectively loaded as in (a). When the muscles are in parallel, as in (c), the load is shared and the muscles can lift twice the weight 2W through their contraction distance d. Note that the work done (2d x W, or d x 2W) in lifting the weight by pairs of muscles is the same regardless of their configuration. Similarly the work done by a muscle depends on the number of contractile units (sarcomeres) within it, and not on the geometrical arrangement.

Movement strength and work

Range of contraction is therefore proportional to the number of sarcomeres in series, or the length of the muscle fibre. The force produced (strength) is proportional to the number of sarcomeres in parallel, or, since the contents of a fibre are predominantly myofibrils, to the transverse sectional area of the muscle fibre. The strength of muscle is approximately 0.3 MN.m–2 of transverse sectional area. Note that the work done by a muscle (force x distance) is the same in both cases (Fig 5.1). The possible work that a muscle can do, or mechanical energy that it can generate, is proportional to the total number of sarcomeres or, in other words, to the mass of the whole muscle.

Consider two activities of a cat. A large force is required to accelerate the mass of the body from the position of crouching, ready to spring. The more sarcomeres that are in parallel, i.e. the greater the transverse area of the muscles brought into use, the greater the acceleration. A cat in this stance arranges its hind limbs and back to recruit as many as possible sarcomeres in parallel (Fig 5.2 a). It also positions each sarcomere at the optimum length for the development of a contractile force (Fig 4.3). You can easily observe this by watching a kitten at play, pretending to stalk and spring.

A galloping cat protracts the forelimbs to lengthen the stride as much as possible (Fig 5.3). This movement demands of the muscles protracting the forelimbs a large range of contraction. The muscle involved must have as many as possible sarcomeres in series.

Fig 5.2 Sarcomeres in parallel

In (a), a cat is crouching ready to spring. The propulsive force will be provided by the extensors of the vertebral column x, and the extensors of the hip y. These are the most massive muscles in the body, and a high number of their sarcomeres are therefore in parallel. The result of the contraction is seen in (b).

5.3 Sarcomeres in series

In the stage of the gallop of the cat in which the forelimb is retracted, the brachiocephalic muscle (dotted line) is fully stretched (a). When the forelimb is protracted, (b) this muscle is fully contracted. During contraction of the muscle, the forelimb is not in contact with the ground; the muscle accelerates only the limb and not the whole cat. The emphasis is therefore on range of movement rather than strength; the sarcomeres in this muscle are therefore predominantly in series.

Each muscle is a unique organ delivering unique torques

Muscle fibres are incorporated into organs, which are recognised anatomically as muscles. These organs are separated by connective tissue sheets or fasciae that permit individual movement. Although several muscles might act over the same joint (for instance there are at least 17 named muscles acting over the hip joint of the dog), each muscle can be defined by its origin and insertion. This endows some joints with a variety of movements (Chapter 8), usually about a point at the centre of an arc about which the joint hinges or rotates. This point is therefore a joint pivot, and the muscles acting over the joint provide turning movements or torques in directions dependent on their skeletal attachments (Fig. 5.4).

Fig 5.4 Torque in the elbow joint

Torque is the product of the force and the perpendicular distance from the pivot it acts over. In this hinge joint, the pivot is in the centre of an arc formed by the condyles of the humerus. The protruding length of the olecranon process of the ulna (d) increases the torque (F x d) that the force (F) produced by the triceps brachii muscle is able to apply to the elbow in attempting to prevent the forced flexion of the elbow joint, as demonstrated here.

Torque and equilibria

Torque is the product of the force and the perpendicular distance from the force to the pivot (Figs. 5.4 and 5.5). The concept of torque is much more useful in estimating the effects of muscles on joints than a concept of levers, since forces often act in an arc about a joint pivot, for a reason already discussed (Fig. 3.3).

In a state of equilibrium, the torques about a pivot balance each other in all directions. These torques usually include that produced by the force of gravity. The torque of postural muscles opposes the gravitational torque.

Fig 5.5 The effect of the site of muscle attachments on the torque produced by muscles over the hip joint

The turning effect of a force about a pivot P, the torque, depends on the magnitude of the force and its perpendicular distance from the pivot d1, d2, d3 or l. In the diagram, the middle gluteal and the semimembranosus muscles turn the femur about the hip bone. Assuming the forces to be equal, the magnitude of the torque is greatest for the superficial part of the semimembranosus muscle and least for the middle gluteal muscle since d2 > d3 > d1. The torques of each of these muscles summate, and produce a propulsive force on the ground. The perpendicular distance of the propulsive force on the ground from the pivot, l, is much greater than the perpendicular distance of any muscle from the hip.

In propulsion, the torque of certain muscles at a pivot results in a force where the foot contacts the ground (Fig. 5.5). The propulsive force at the foot is less than the force of muscle contraction. The advantage is, however, that the range of movement at the foot will be greater than the range of contraction of any of the muscles. The power for propulsion comes from a concentration of forces about the hip (Fig. 5.2). Use the concept of torques to consider how limb design must optimise the muscular forces that accelerate hip extension, while optimising stride length. The properties of limbs are discussed further in Chapter 8.

5.6 Strap muscles

Diagrammatic representations of two muscles of similar mass but different shape. Mechanical values are given for the muscles relative to 100 for the muscle a. The “functional transverse area” is indicated by the dotted lines. Tendons of origin and insertion must be related in thickness to the strength of the muscle in series with them.

Fibrous architecture of muscles

An equally important aspect of design affecting strength and range of movement of muscles is their fibrous architecture. Here, "fibrous" refers not only to muscle fibres, but to collagen fibres also. In the simplest case, fibres within the muscle are aligned parallel to the force vector of the whole muscle. Such muscles are called strap muscles (Fig. 5.6). Their range of contraction and their strength depends on their shape, because this determines the number of sarcomeres in series or in parallel. Only one combination of range and strength will fit into a particular space in the body. The use of strap muscles in musculoskeletal design is therefore limited.

Muscles of the same shape can behave very differently Figure 5.7 compares three muscles of the same mass, and the same general shape. Each of these muscles could fit into the same space in the body. If the fibres are parallel to the force vector of the whole muscle (Fig. 5.7 a), the number of sarcomeres in series is maximal, and the number of sarcomeres in parallel is minimal, for a muscle of this shape. The fibrous architecture of such a strap muscle gives maximal range of movement, and minimal strength.

If the fibres are aligned at an angle to the force vector of the whole muscle (Fig. 5.7 b, c), the effective force and range of movement of each fibre is reduced since it is proportional to the cosine of this angle. Compared with Fig. 5.7 a, the number of sarcomeres in series has been reduced, and the number of sarcomeres in parallel has been increased. Thus the force has been increased in spite of the angulation of the fibres, but the range of contraction has been decreased. In the direction of the fibres, the work done during contraction is similar for the three muscles, since their mass is the same.

Fig 5.7 Pennate muscles

Diagrammatic representations of three muscles of similar mass but different shape but of widely varying fibrous architecture. Approximate values for range of contraction, force and work are given for the pennate muscles b and c, relative to those of the strap muscle a = 100, when the angle of pennation  = 25°. The "functional transverse area" is indicated by the dotted lines. Note that the effect of pennation has been to reduce the range of contraction and the work effective in the direction of contraction, but to increase the force. Note also that the more sarcomeres that are in parallel within the muscle, the more tendinous apparatus must be in series with it.

Fig 5.8 Extremes of pennation

The properties of a muscle vary with the proportion of collagen built into its architecture, even though its external appearance, as judged by its shape and size, remain much the same.

Some muscles look like feathers

Muscles with the fibres at an angle to the force vector are termed pennate (L. penna, feather). Not all the work done in this type of muscle is useful in the direction of action of the muscle. Tendons of pennate muscles may be central (Fig. 5.7 c) or they may form a tendinous sheet on the surface of the muscle (Figs. 5.7 b, c), called an aponeurosis (Gr. apo, from; neuros, nerve) because the ancient Greeks did not distinguish properly between nerves, ligaments and tendons. The appearance of the fibrous connective tissue of an aponeurosis may at first give a misleading impression of the arrangement of the muscle fibres within.

Pennate muscles need this collagenous framework to link the increased number of sarcomeres in parallel. Also, because of the increased force of pennate muscles, there must be a proportionate increase in the strength, and hence the transverse sectional area, of tendons of origin and insertion (Fig. 5.7).

When muscles become ligaments

With increasing pennation, the range of contraction decreases and the strength increases (Fig. 5.8). The limit is reached when the muscle fibres become too short to function and the muscle becomes entirely ligamentous. This occurs in certain muscles as an effect of body size (Chapter 7). How do contracting muscles fit into a limited space? Pennate muscles change shape during contraction in a manner different from strap muscles. A contraction of a strap muscle by 30% results in an increase in transverse sectional area of 30% since the volume of the muscle is constant. On the other hand, it is possible for a pennate muscle to contract without an increase in the transverse sectional area of the muscle (Fig. 5.9). This is important where muscles must lie in a constricted region, such as within the antebrachial or crural fascial sheaths.

Note that the decreased range of movement of a pennate muscle can be compensated for by an appropriate change in its skeletal attachments. (Fig. 5.5); a strong pennate muscle, such as the deep gluteal muscle, can still deliver an effective propulsive force at the foot even though its force is directed close to the pivot at the hip.

Fig 5.9 Contraction of a pennate muscle

A fibre maintains a constant volume during contraction. Its areas of attachment to the tendons of origin and insertion are also constant. This figure shows a single muscle fibre with solid outlines in only two dimensions, stretched in (a) and contracted in (b). The following argument is, however, correct for a three dimensional structure. Because the area of the parallelogram shaped fibre is constant, its length of attachment x is constant, and its area is x. y, y = y'. Therefore although the individual fibres of the muscle increase in thickness during contraction, the pennate muscle as a whole does not.